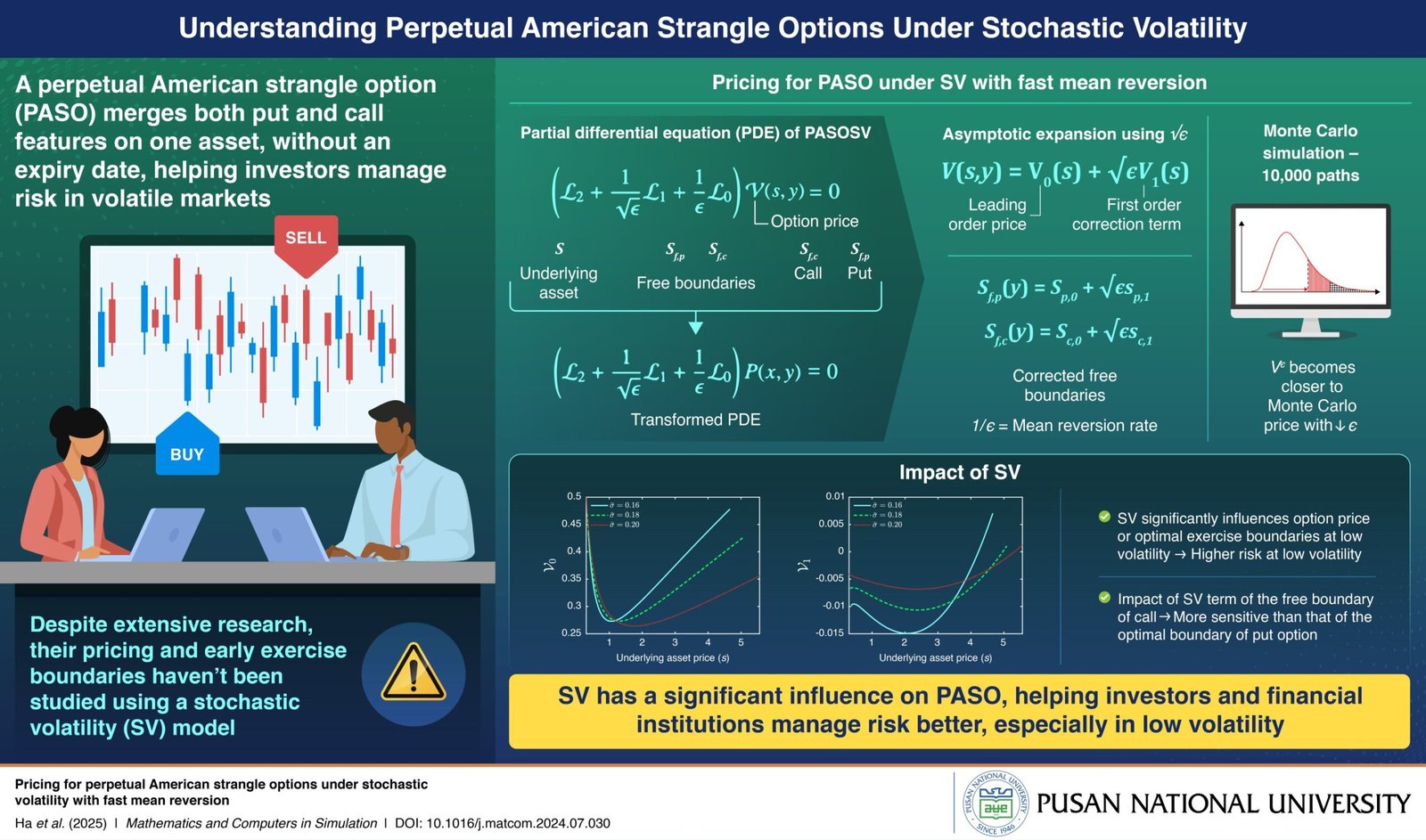
Perpetual American strangle options (PASOs) offer investors a method for minimizing risk during highly volatile market scenarios by allowing them to buy or sell options at any date without an expiration date. In a new study, researchers investigated the pricing of PASOs under a stochastic volatility model with fast mean reversion which better captures real markets compared to traditional models.
Options are a financial instrument that gives the holder the right to buy and sell an underlying asset, at a predetermined price, on or before a specified date. For example, European-style options allow the buyer to exercise this right at its maturity date, while American-style options can be exercised at any time up to and including the expiration date. These are generally traded in public financial markets, such as stock exchanges.
With the increasing complexity of markets, a wide range of products have emerged, including strangle options. A strangle option is an investment strategy that combines call and put options, both with the same expiration date but different strike prices. This strategy is typically used by investors who anticipate a large fluctuation in the market in either direction, as it helps minimize potential losses.
PASOs take this further by allowing the holder to exercise the options at any time, without an expiration date, providing considerable benefits. Consequently, PASOs have been the focus of considerable research. However, despite such studies, the pricing of PASOs and their early exercise boundaries have not yet been studied using a stochastic volatility (SV) model, which more accurately captures real market behavior compared to the Black-Scholes model.
Addressing this gap, a team of researchers led by Associate Professor Ji-Hun Yoon from Pusan National University, Korea developed a pricing formula for PASOs under an SV model with fast mean reversion. Their findings were made available online on July 27, 2024 in Mathematics and Computers in Simulation.
“In recent years, financial markets have experienced considerable fluctuations during global financial crisis, such as the US subprime mortgage crisis in 2007 and 2008, the Eurozone crisis in 2010, the COVID-19 pandemic, and the Russia-Ukraine conflict. American strangle options can help investors minimize risk during such crises,” says Dr. Yoon.
In this study, researchers first established a partial differential equation (PDE) for the value of PASOs under an SV model (PASOSV). A PDE is a mathematical equation that helps to model how one variable changes with respect to another.
In this case, the value of the PASOSV relative to the underlying asset’s price. However, due to the complexity of SV, an exact solution was not possible. Instead, the researchers applied an asymptotic analysis approach, incorporating a special term representing the fast reversion rate of highly volatile markets.
To validate their formula, they used the Monte-Carlo simulation method, which predicts potential future values of assets through thousands of simulated scenarios. They also conducted numerical simulations to analyze how SV impacts the option price and the free boundary values using various parameters. The findings revealed that SV significantly influences option prices and exercise boundary values when volatility is low, indicating that while high volatility can give higher returns, low volatility can increase risk from investing in PASOs.
“Our study lays the foundation for development of more resilient products by financial institutions, thereby providing investors with better tools and strategies to manage risk and maximize returns, especially in low volatility environments,” concludes Dr. Yoon.
More information:
Mijin Ha et al, Pricing for perpetual American strangle options under stochastic volatility with fast mean reversion, Mathematics and Computers in Simulation (2024). DOI: 10.1016/j.matcom.2024.07.030
Provided by
Pusan National University
Citation:
Researchers develop precise pricing formula for perpetual American strangle options (2024, September 16)
retrieved 16 September 2024
from https://phys.org/news/2024-09-precise-pricing-formula-perpetual-american.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.